
のもと物理愛のケプラー回で懐かしの楕円が出てきた。太陽系の惑星の軌道は楕円という歴史的大発見と3定理の話だ。50年ほど前、高校生だった私はその定理を知ったときに心がふるえたことを覚えている。いったいどんな発想があれば、惑星の軌道が楕円だと導けるのか、そして太陽がその楕円軌道の焦点にあることがわかるのか。
楕円っていいよな、懐かしいなあ〜と感動しつつ、ふと楕円の式を導いたことがないことに気づいた。楕円好きならそれぐらいはできないとダメだ。いっちょやってやろうと決意した。
楕円は高校数学の試験ではあまり出てこなかったので、未知の領域だ。ただその式は知っている。そして、2つの焦点から周に引いた線分の長さの合計が常に等しいことを聞きかじっている。どこで小耳に挟んだのだろう。楕円の作図は2本の棒を地面に立ててロープを結んで・・・というような逸話だろうか。
まずは、その作図の方法から楕円の式を導くことにした。
私は勉強好きではない。50年前から不真面目でずぼらだ。布団にはいって寝付く前に暗算でいこうと思った。三平方の定理の登場だ。デカルト座標で、短半径と長半径の長さをa、bとして、周がY軸、X軸上にあるときの焦点を結ぶ線分の長さは簡単に出てくる。楕円の周(x、y)の線分の長さもa、bで示すことができる。
この3点がa、bで示せるんだから、なんとかなりそうだ。この思いつきには我ながら「やるなお前!」と布団の中で思った。
ただ実際にやってみると難しくてやってられなかった。数式が見えてればすんなり行くかとおもいきや、何度やってもあり得ない解が出てくる。今にして思えばルートの計算とか式の変形にミスがあったのだ。とにかく時間がかかるったらありゃしない。しまいには三平方の定理で愚直にやるだけではダメなのか?何かひらめきが必要なのか?と疑心暗鬼になった。
結局、観念してxの値が焦点にあるときのP(x、y)なら簡単な式になるので、それでやってひとまずの解決を得たのだった。
しかしながら、楕円の周(x、y)がどこにあっても、焦点を結ぶ線分の長さが一定ということから、楕円の式を導きたい。計算が難しいのがよくないので、ちょっと細工をして、長半径を1、短半径をaとした。
これでも、全ての楕円が描ける。また、第一象限だけやっても、他の象限は対称にすぎないのだからOKだと思った。
これではどうにも結論先取してトートロジーをやらかしているようで不安だ。楕円の式をあらかじめ知っていないと導ける気がしない。このあたりが私の限界。
ともあれ逆方向からなら、つまり楕円の式からならLは一定であることが導ける。
2つの焦点と周を結ぶ線分の長さLが一定のとき、その周は楕円だというのは楕円の定義だと思っていたが、次第に怪しいと思い始めた。それはやっぱり素直ではなく、楕円を地面に描くための方便じゃないかという気がする。
この世の中にはもっと自明な楕円がある。たとえばマンホール。自転車を走らせていると無数のマンホールがあって、滑るのは危険だしガタが気に障るので、注意して避けることになる。マンホールの蓋は円であるから、それを斜めから見たのが楕円のはずだ。これがもっとも定義らしい定義。
それを証明したい。
2つの焦点と周上の点を結ぶ2線分の長さの和が一定になる図形は楕円である。この定義は自明ではないから、楕円は傾いた円、または一定の値aで押しつぶすか引っ張るかしたのが楕円。こう定義したほうが感覚的にマッチする。
そして「焦点」という名前がついているからには、その2点にはもっと秘密がありそうだ。その秘密については、焦点から周に向けて放つレーザービームは反射してもう一方の焦点に当たる、というのが当てはまると思った。40年ぐらい前にそんな定理を聞きかじったような記憶もある。
たぶんそれは真だろうから、いっちょ確かめてやろうと思いついた。
焦点Fから周上の点P(x、y)に放ったレーザービームが跳ね返る、というのは点P上の接線とFを結ぶ線分の角度が反射するビームの角度に等しいということだ。まずそこを考える。
楕円の接線というのは少しとまどったけれど、楕円に外接する円を考えて、Fから足を伸ばして円周との交点を求めて円の接線を引く。それを押しつぶして楕円に重ねれば、楕円の接線になると思った。そうすれば点Pの値もとれるし、レーザービームも一次方程式として座標上にかける。そこまでくれば証明はできそうに見えた。
しかし、図は描けても角度をどうやって測るかが思いつかなかった。できないことだけは簡単にわかったから、代替手段を考えていると、角度が解らなくてもsinθが同じなら角度も同じということに思いついた。
それならば、直角三角形を作図して必要な点はすべてだせるし、点と点の距離も計算できる。いけそうに思った。しかし実際にやってみると、2点間の距離の式が複雑過ぎて手に負えなかった。私には無理だから、楕円を固定して、ひとまず点Pも特殊なものでやってみて予想が正しいかどうかを確かめることにした。
予想の確からしさは明らかになったとはいえ、物足りなさは残る。物足りなさはふとしたときに心に浮かんできて、眠りにつけなかったりする。布団の中で数時間あ〜でもない、こ〜でもないと考えて、代数ではなく幾何(中学校のときは図形問題といってた)にすれば解けるんじゃないか? という気がしてきた。
計算を簡単にするために、円を半分に押し縮めた楕円でやってみると首尾良く解けた。
2点間の距離を出すのに三平方の定理を使う関係上、式は複雑になるけれどギリギリ手に負える範囲だった。
いろいろ作図をしてレーザービームの検討をしていると、妙な事に気づいた。
楕円周の接線に向け、焦点Fから垂線の足をおろすと、その交点が必ず楕円に外接している円上にありそうなのだ。最初の1、2回は、そんなのたまたまで、ちょっとはずれてるに違いないとわざと円周から外すように補助線を引いたものだ。
それがいろいろな楕円、いろいろな接線で幾度となく作図するうちに定理ではないか?という気になった。となれば調べればよい。これも1/2につぶした楕円の第一象限についてやることにした。交点Aの値がなんだかたいへんなことになって、もしかして無理?とも思えたが意外にもあっさりできた。
楕円のレーザービームの問題は三角形の相似を使って首尾良く解くことに成功した。しかしxy座標で直線の交点を使って数式で解くやりかたが心に引っかかっている。それがもっとも簡単愚直な方法だからだ。
夜中なんかにふとアイデアが湧いてくるともういけない。いろいろ迷って、係数がなるべく単純な方法なら解けそうな気がした。2点間の距離を求めるのは無理なことが解っている。そこを回避するためのすばらしい補助線がひらめいた。下図のマゼンダ線である。
Aを通り、青線に垂直な緑線。青線に平行でx軸上のCを通るマゼンダ線。AとBを結ぶレーザービーム(赤)の反射線。
脳内イメージで3つの補助線を引いて、これはいけると布団の中で確信した。こうすれば、交点Eと交点Dのyの値だけを求めればよい。CEの中点がDであれば、角α=角βとなるのだから、それぞれの交点から垂線の足をx軸に降ろして、EE’がDD’の2倍であればよいのだ。これなら前の方法よりも圧倒的に計算がやさしい。
というわけで紙と鉛筆をいそいそとりだして、3つの線の式をさくさくと立てた。赤線のABの式がかなり怪しげでぞくっとしたが、これらの式で連立方程式を作って、交点D,Eそれぞれのyの値を求めた。
楕円研究の手始めは、2つの焦点から周に引いた線分の長さの合計が常に等しいことから、楕円の式を導くことにあった。一応それなりのことはやって、先に進んだものの、煮え切らない気分が残っていた。
楕円の式を使わなければ楕円の式が導けないってかっこ悪い。まるで楕円の式を知らなかったかのように、線分の長さの式を変形して整理したら楕円の式が得られたって体裁はとれないものか。いろいろやってはみたものの、どうにならない。2つの√を足し算するところがネックだった。原理的不可能なんだろうとあきらめて一年ほど放置していた。
それが2025年1月16日にひらめきが降って湧いた。聖マリアンナ医科大学横浜市西部病院の待合室で順番待ちをしていると、窮地を突破できるアイデアがぽっと心に浮かんだのだ。楕円のことを考えていたわけでもなく、女房と二人で高島礼子のビデオを見ていたときだ。
ひらめきとは、「両辺に√を1個ずつなら、両辺を2乗すりゃ√が1つにできるよね」ってことだった。そのテクを使えば、暗算で道筋が見えた。
「2つある√の1つを移項して両辺を2乗する」なんてテクは受験生だったころなら普通に使っていたのだろう。そのあたりの記憶はまったくないが、降って湧くくらいだから身についてたんだと思う。
楕円のレーザービーム問題は、楕円の短半径を1/2にすることで首尾良く解くことができた。むろん短半径をaとしなければ解いたことにはならないのだが、計算が難しくてあきらめていた。しかし、脳裏でくすぶっている問題があきらめきれるものではない。ダメでもあきらめきれないのが恋だから。
変数が、pとqで定数が、aとf、4つの記号がちりばめられた式を変形し整理して計算しなければならない。ほんのちょっと狂うだけで数式はとんでもないことになってしまう。原理的に解けない問題ではないはずで、考え方もあってるはずだ。
pとq、aとfはそれぞれ一方が決まれば他方も決まる。臨機応変に変換すべきところを選択しながら記号の種類を減らしていくのがみそだと思った。検算しながら式と計算の間違いをつぶしていった。検算でも間違いが多発したことは言うまでもない。
1週間ほどやってみて手に負えないと正直思った。その原因は、単なる計算ミス、記号の書き間違いなどのケアレスミスだった。計算力はもともと低かったが、ここまでダメになっているとは。正解を得て感じたのだが、正しい筋道を行けば計算は簡単だった。この問題の計算が√を使わなくても可能だということは驚愕だ。
解けた喜びよりも、衰えの寂しさのほうが大きい。ここにこうして記載することで、こんな難しそうな計算もできてたのか、信じられない・・・と感慨にふけるときも遠くないだろう。
ここまで来たんだから、ついでに図形問題の方法でも解いてみようと思った。
こちらの計算は容易だろうと予想はしてたものの、予想以上だった。大学受験の数学の問題みたいに、するすると解けてしまった。受験の数学は短い試験時間用に作ってあるから、こんなんだったなと懐かしい。
今回の楕円研究で一つやり残していることがあった。「楕円に接する直線と、それに直交して焦点を通る直線の交点は楕円に外接する円の周上にある。」という命題の証明だ。こんな命題は過去に聞いたことがない。楕円のことをいろいろ考えるうちに、ひっかかり、独自に発見した命題だ。
すでに、円を半分に縮めた楕円ではこの予想が成り立つことが証明された。しかし、どんな楕円でも成り立つことが証明されなければ、これを定理と認めることができない。
その証明は困難だろうと予想された。考え方はとっても簡単シンプルだが、計算が難しいのだ。この度、その困難を克服して解決に至った。
この証明は単純だが、困難の極みだった。一次方程式の勘違い、分数とか正負で起きる単純なミスが命取りだ。こうして正解を得れば、一本道の計算に過ぎない。ところが、正負の記号を一つ間違えたり、分子と分母が入れ替わってたりすると、とんでもない方向に計算が進み、手がつけられなくなる。
正しい道を歩んでいることを確信できないと、疑心暗鬼になって計算ミスも起きる。
疑心暗鬼をなくすために、計算途中の式にあるaとpに適当な値を入れて、答え合わせをする必要があった。初期には電卓でやっていたが、そもそも電卓初心者で、誤りが式にあるのか、電卓計算にあるのかが不明になってしまった。かといって関数処理ができる計算機は持っていない。
そこで持ち出したのがエクセルだ。エクセルでは計算式を手順を追ってセルに記述できるから、解がおかしなことになっていれば、遡って式の修正ができる。
エクセルの入力ミスは多発して、正しい式を書くのに半日かかった。苦労は多かったが、aとかpとかに、0.2、0.3、0.8、0.1・・・とランダムな値を打ち込んでも、x^2+Y^2が貼りついたように1を表示していると本当にうれしかった。私はエクセルが好きかもしれない。
偶然発見した直交定理だが、そもそもそれはどんな意味があるのか。「楕円の接線に向け、焦点から降ろした垂線の足は、楕円に外接する円の周上で交わる。」こう書くと無意味な、〜ですがなにか? に思える。
しかし、上図を参照すれば一目瞭然に気づくように、「そもそも楕円の焦点って何? 焦点はどこにあるの?」という疑問の解答が直交定理だったりする。
Y軸と楕円が交わる点に接線(青線)を引いて、その接線と外接円の交点から、X軸に降ろした垂線(緑線)の交点が焦点だからだ。けっこう重みのある定理だと自画自賛してみる。
ついでに、楕円と円の交点上に接線を引けば、垂線の足である緑線はX軸上にある。この場合なら青線と緑線が直交していることは自明だ。
さらに上図。単に円の中心から円周に向かう直線の交点に接線を引いただけの図だ。直感的にも2つの直線は直交している。その証明や応用問題は義務教育で頻繁に出てくるから日本のいい大人は習知だ。
しかし、これに楕円が隠れていることを知る人は少ない。Y軸上の(0 , a)の値を1にどんどん近づけると楕円は円に重なる。同時に2つの焦点は近づいて来て、円の中心に重なる。したがって、これでも「楕円の接線に向け、焦点から降ろした垂線の足は、楕円に外接する円の周上で交わる。」という定理は生きているのだ。しかもややこしい証明は無用だ。
すでにお気づきのように、楕円研究で見てきた全ての定理、「2線分の合計長は一定」「レーザービームは反射してもう一方に焦点に当たる」・・・そして接線の直交定理も、楕円を円とするなら、全て直感的に理解できる。円はなんと美しく優しくて完璧な図形なんだろう。
さて楕円好きならここで、のもと物理愛の『パウリの排他原理』の回で言及された、ゾンマーフェルトの名言を思い出さなければいけない。曰く、『円は楕円の特殊ケースに過ぎない。』この言葉に楕円好きの私はニヤリとしてしまう。よくぞ言ってくれた。完璧な円に対して“〜に過ぎない”と。
惑星、衛星の公転も原子核の電子の軌道も楕円だ。自然界の主流は楕円。地球だってちょっと中ぶくれの球らしい。もしかしたらみんな円になりたいのかもしれないけれど、諸事情あって楕円になっている。マンホールとか道路標識とか、私が円だと知覚しているものも、目に写っているのは楕円だ。厳密に円に正対することはできないから。人間はプラトンのイデア的理想の元で円を夢見ている。
ところで、楕円の周の長さがよくわからない。それぐらいはできないといっぱしの楕円好きとは言えないだろう。ひとまず楕円の公式がわかったところで、周の長さにチャレンジだ。
それはとっても険しい道のりだ。真円であれば、正多角形と三平方の定理から近似していく方法を中学か高校で習った。同様の方法を楕円で夢想してみたが、どうにも難しい。もっと簡単かつエレガントな方法があるはずだ。
まず思いついたのは、円と楕円に内接するひし形の長さの比が、円と楕円の長さの比に等しいだろうというアイデアだ。それで周の公式が導けるかもしれない。
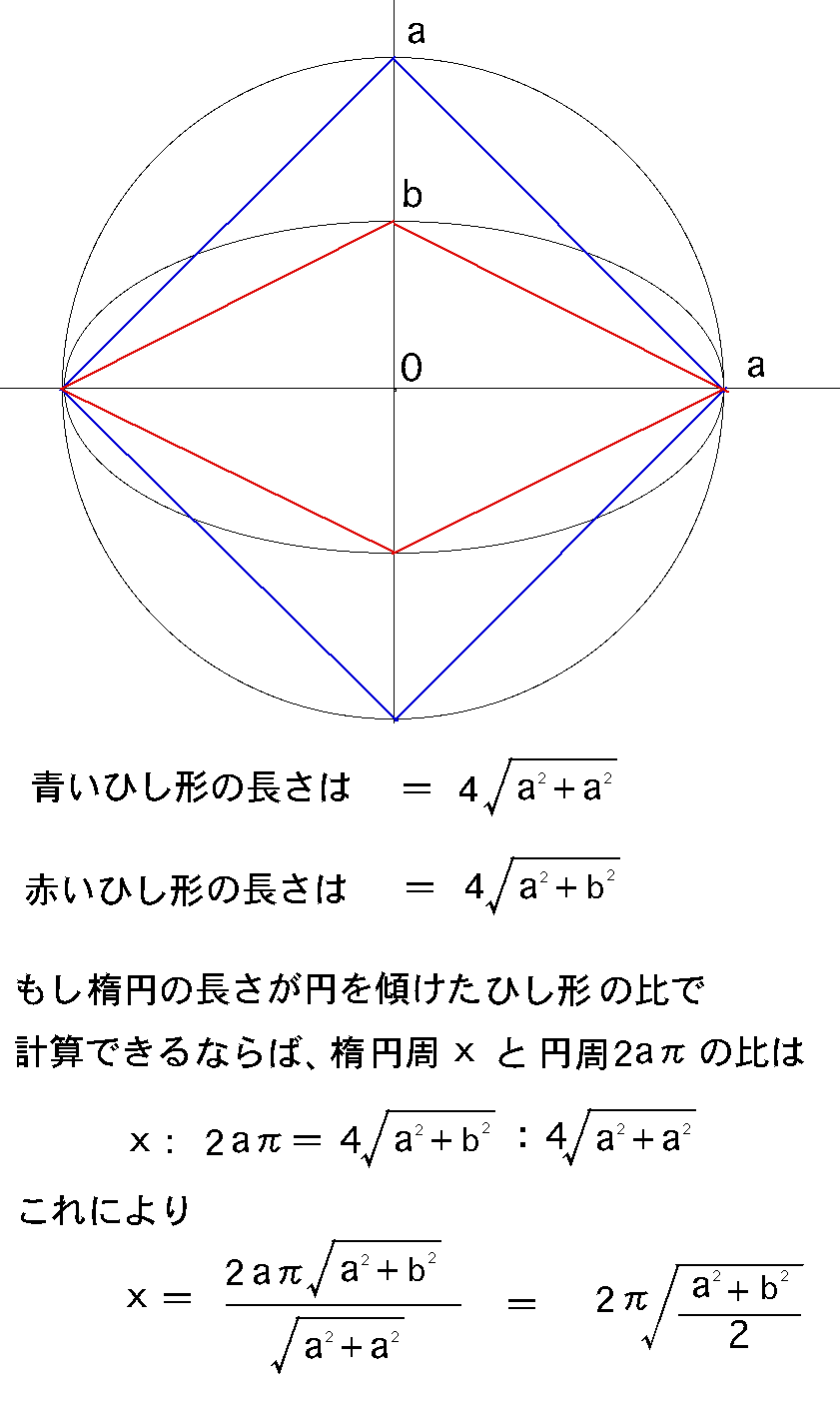
一見正しそうにも見えるが、これは明らかに間違っている。楕円の場合、即座に判明する周の長さが2つある。a=b、いわゆる真円のときと、b=0、線分にまでつぶれたときだ。この解き方だと、a=bのときは正しいが、b=0のときπが消えないからだめだ。だめな理由ははっきりしないけれど、だめなことだけはわかった。
b=0のときπを消す方法はπをb乗することだ。そしてb=aのときにπを無傷で残すためには、πをb/a乗すればよい。これはうまい手だと思うのだが、なにぶんπ^(b/a)の意味がわからない。いろいろ想像をたくましくするものの、なんの着想も湧かなかった。
ここいらで一つ初心に戻って愚直な解法を試すべきだと思った。実際最初は古代ギリシャのアリストテレスたちが得意にしていた三角形を作って突き詰める方法を真似ようとしていた。ただし、どうやっても壁に当たる未来だけが見えていた。
そしてとうとう私でもできそうなやり方に辿り着いた。図のような楕円を作図してBからAに赤線を引く。この赤線の長さは、BからAまでの楕円周長よりもかなり短い。だけど線分だから、三平方の定理ですみやかにその長さはわかる。赤線=((a^2)+(b^2))^(1/2)だ。
次に、X軸上のa/2(長半径の中点)から垂線を伸ばして、楕円との交点をPとする。BP、PAの2本の赤線分を合計すれば、楕円の周長にもう一歩近づく。Pの値を求めることは楕円の公式があるから簡単だ。BP、PAの長さも、先と同様に三平方の定理で求めた。
さらにもう一歩、OAを三等分して、楕円上の点P1、P2をとり赤線を引くとさらに楕円の周長に近づく。P1〜P2はちょっだけ赤線の長さを求めるのがややこしくなるが、この調子でP1、P2、P3、P4、P5・・・・と進めて行けば近似値が得られるはずだ。
OAをn分割して式を立て、n=∞にしたときに、a、b、nの式ができれば、それで大願成就となる。それをイメージするぐらいの数学力はある。だが、大きな懸念があった。πの不在だ。楕円の式がπなしで成立するとは思えない。この先に進めばどこからかπが現れるだろうか。
布団の中で考えをめぐらせ良いひらめきを得た。a=b=1(*半径1の真円)のとき、楕円周ABは1/2πになる。すばらしい朗報だ。ということはこいつはπの近似値を求める方法でもあるのだ。いつかきっと私の式はπに出会えるに違いない。
やることは、C0(Y軸上の点B)からCn(原点)までの値を順次求め、三平方の定理を使って赤線分P0〜P1、P1〜P2、P2〜P3、P3〜P4・・・P(n-1)〜Aの長さを求め足し上げて行くだけのことである。一般値のCkも簡単な計算で出せる。これで、Ckと(k*a)/nの2つの値が求められる。そしてnを無限大とはいかなくても、できるだけ大きな値まで計算すればよいのだ。
いうまでもなく、私が電卓で計算したりすれば、n=20程度でも1年以上かかるに違いない。ここはちょっと好きかもしれないエクセルにご助力いただくことにした。入力と計算をもっと楽にするために、a(楕円の長半径の値)は1にした。表計算ってのはホント天才的発明品だ。
ひとまず、a=b=1の真円、長半径を分割するnは40にして検算してみることにした。この場合、図にある楕円は真円だから周長さは半径1の円の4分の1に等しくなる。図上、赤線で表した多角形の長さは、π/2(1.5708・・・)に近づくはずだ。
やってみれば、SUMは1.57021となり、予想通りπ/2より少し小さくなっている。やり方は正しいのだ。円で合っているのだから、これを楕円にしても正しいだろう。私はついに任意の楕円の周長を求める方法(エクセルのシート)をゲットしたのだ。
だがしかし、近似値を求める計算式を一行にする方法はわからない。私が見たことも聞いたこともない高等テクニックがあればaとbとπであらわされるエレガントな式が導けるのだろう。kが入れ子になっているnの級数なんて無理難題だ。そして今回の方法ではπの影も形もない。まあ偶然にもπの近似値を求める方法に逢着したのだから、良しとしよう。
到達点としては、長半径aと短半径bとπからなる数式になるはずだ。そうでなければ、楕円の周長を求める式とはいえない。先のやり方でπを潜り込ませる裏技を発見した。オリジナルな着想ではない。ユーチューブでオイラーのバーゼル問題を幾何学的に解くという解説動画がヒントだった。
πといっても定数なんだから、長半径にπを潜り込ませれば、πを私の解法に取り込める。長半径を1/πにすれば、外接円の円周は2となってなんだか計算も易しそうだ。半径にπを入れるってのは、コペルニクス的転回、一休とんち話的な窮鼠猫を咬む大逆転技ではないか。
そう思って、まずは暗算にかけてみたものの、なんの進展もないことが明らかになった。所詮定数は定数でしかないのだ。やはり私のような非力な人間には楕円の周長なんて高値の花。雲の上の存在として手の届かないところにあるのだろう。
暗算していてπを出す別なアプローチに気づいた。半径ではなく焦点を利用する方法だ。楕円の作図では、2本の棒を立ててひもをゆるく結び、ひもを引っ張りながら周を描く方法がある。2つの焦点と周上の1点を結んだとき、2本の線分の和が常に一定になることを利用した作図法だ。
この性質を使えば周長が求められるのかもしれない。ひもの長さをほぼ無限大にすれば、その楕円は真円になる。つまりπがでてくる。逆にひもを最短にぴんと張れば、その楕円はほぼ線分となる。つまりπが消える。
ただ私の力では、その解法のとっかかりすら見えない。無理難題である。